안녕하세요, 이번 포스팅에서는 Graph-based Semi-Supervised Learning에 대해 알아보겠습니다.

본 내용은 고려대학교 산업경영공학과 강필성 교수님의 강의와 강의자료를 바탕으로 작성됐음을 밝힙니다.

(https://github.com/pilsung-kang/Business-Analytics)

또한, 본 내용은 먼저 이론 내용 전체를 살펴본 뒤 그 이론에 대한 독자의 이해를 바탕으로 Python Code를 살펴보고 마지막으로 요약하는 방식으로 구성돼 있습니다.

자, 그럼 이제 시작해볼까요?

Semi-Supervised Learning

Graph-based Semi-Supervised Learning을 알아보기 전에, 먼저 Semi-Supervised Learning이란 무엇일까요?

Semi-Supervised Learning이란 Machine Learning(기계학습)의 한 학습방법입니다.

그리고 기계학습의 다양한 학습방법 중 대표적인 세 가지 방법을 들면, 아래의 그림과 같이 Supervised Learning과 Unsupervised Learning 그리고 Semi-Supervised Learning을 들 수 있습니다.

기계학습에 필요한 Data는 x변수(독립변수 또는 예측변수 또는 입력변수) 또는 y변수(종속변수 또는 반응변수 또는 출력변수)로 이루어져 있습니다.

각 학습방법을 구분하는 기준은 Data의 구조(Structure)입니다.

y변수의 instance가 x변수의 instance 개수만큼 전부 존재하는지, 전부 존재하지 않는지, 아니면 일부만 존재하는지에 따라 적용할 수 있는 기계학습 방법이 다릅니다.

그리고 각각의 기준으로 Supervised, Unsupervised 그리고 Semi-Supervised Learning으로 나뉩니다.

이때, y변수는 연속형 실숫값이 될 수도 있고 범주형 값이 될 수도 있지만, 본 내용에서는 범주형 값(class label)을 기준으로 설명하겠습니다.

Supervised Learning은 모든 label 값을 알고 있는 상태에서, 사용자가 가지고 있는 Data를 충분히 잘 설명함과 동시에 새로운 Data(x변수)에 대해서도 잘 labeling(y instance) 할 수 있는 모델(y=f(x))을 학습하는 방법입니다.

Unsupervised Learning은 label을 전부 모르기 때문에, 사용자가 가지고 있는 Data의 내재적인 속성을 학습하여 label을 찾을 때 사용합니다.

마지막으로 Semi-Supervised Learning은 Supervised Learning처럼 label이 없는 새로운 Data에 대해 잘 labeling 하는 모델(y=f(x))을 학습하는 방법입니다만, 학습할 때 label이 없는 기존의 Data도 Input으로 함께 활용합니다.

그리고 어떻게 활용하면 성능이 향상될지 고민하게 됩니다.

즉, label이 없는 Data라도 그 Data들을 학습 과정에 추가하면 무엇인가 조금 더 좋아지지 않을까? 라는 기대에서 시작된 것입니다.

Semi-Supervised Learning vs. Transductive Learning

앞에서 설명했듯이 Semi-Supervised Learning은 ‘새로운’ Data에 대해서 잘 labeling 하는 것에 관심이 있습니다.

반면에 Transductive Learning은 모델을 학습하는데 사용된 ‘기존’ Data 가운데 label이 없는 Data의 label이 무엇인지에 관심이 있습니다.

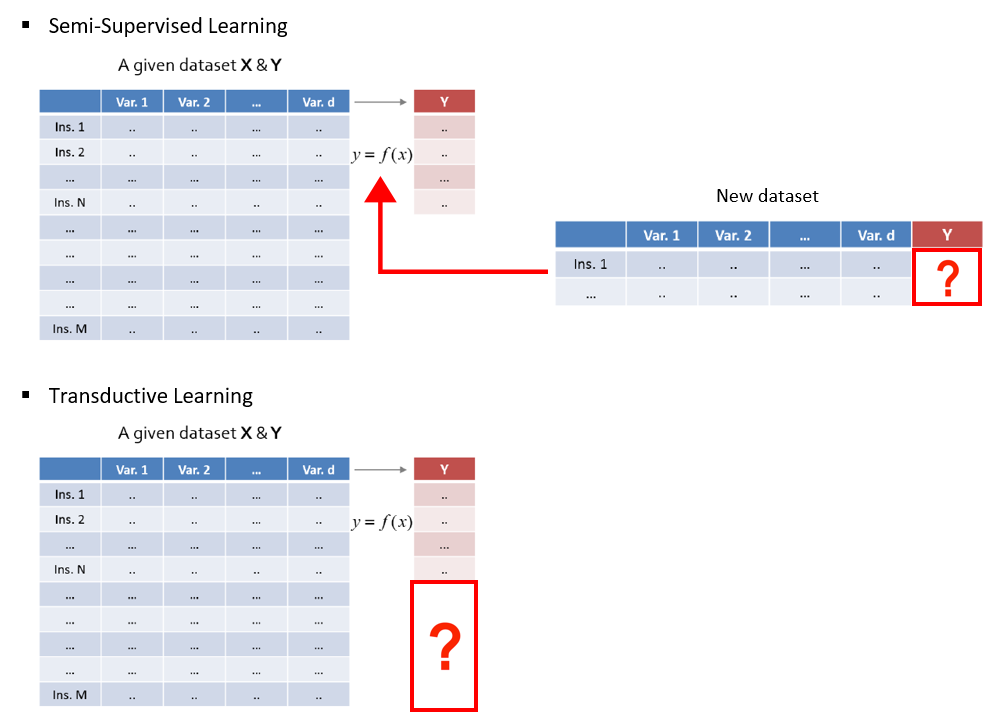
Semi-Supervised Learning처럼 labeling 하는 것에 관심이 있는 것은 같지만, 그 대상이 모델을 학습하는데 사용한 label이 없는 Data, 즉 Unlabeled Training Data라는 것이죠.

이처럼 두 방법은 서로 다른 개념이지만, 많은 사람들이 두 학습방법을 섞어 쓰기 시작하면서 그 경계가 허물어졌다고 합니다.

그럼에도 불구하고 두 방법을 엄밀히 구분하여 설명한 이유는, Graph-based Semi-Supervised Learning이 Transductive Learning이기 때문입니다.

Dataset의 Graph Node 화 및 Node 간 Indirect 연결 방식

먼저 아래의 그림을 보면,

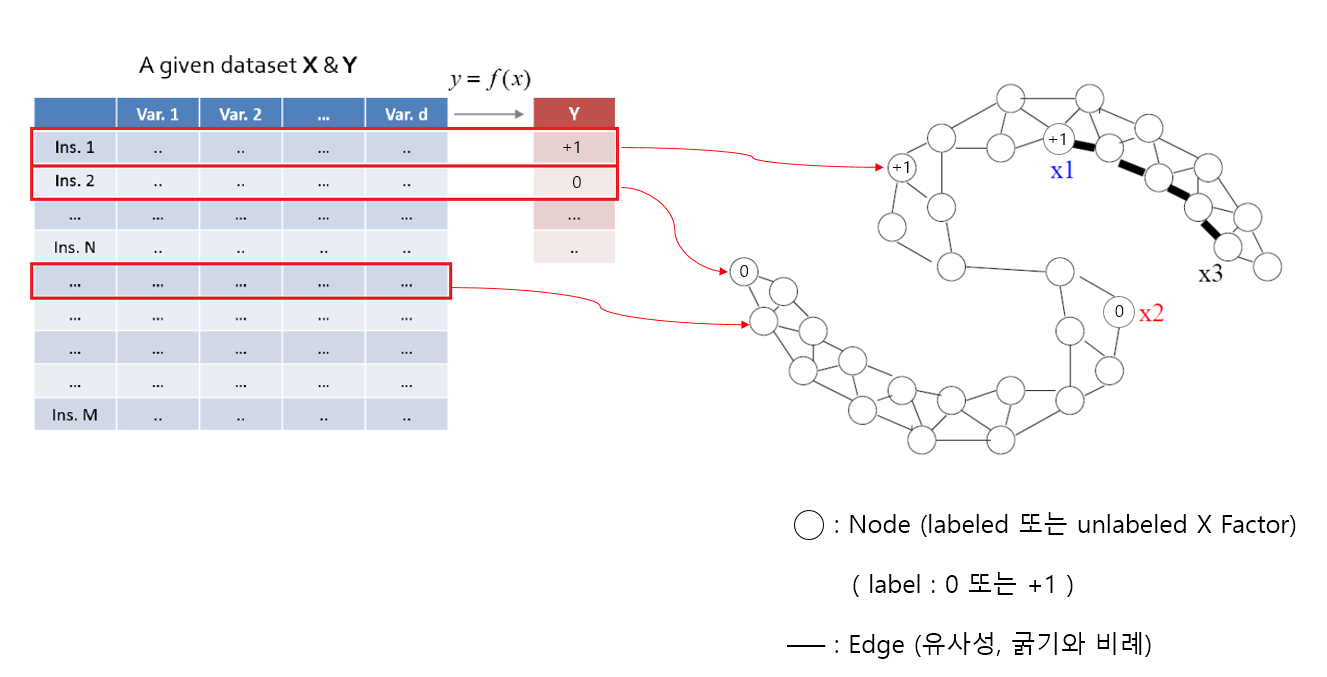
주어진 왼쪽의 Data Set에서 instance 단위로 오른쪽 Graph의 Node에 할당되는 것을 알 수 있습니다.

이는 각각의 instance를 Graph에서 Node로 표현하는 방식임을 알 수 있습니다.

이때, label 값이 있는 instance는 해당 label의 값이 Node에 나타나고 label 값이 없는 instance는 label 값이 없는 빈 Node로 남게 됩니다.

그리고 Node 간 연결된 선들을 Edge라고 하는데, 이는 Node 간 유사도(similarity)를 나타내고 연결된 Node 간 유사도가 클수록 굵은 선으로 나타냅니다.

예를 들어, 이미 label이 있는 x1과 x2는 서로 다른 label이기 때문에 Node 간 연결돼 있지 않습니다.

반면에 label이 없는 x3 Node의 label을 추정하는데, +1 label 값을 갖는 x1 Node로부터 시작해서 굵은 선을 따라 추정하게 됩니다.

하지만 이때, x1 Node에서 x3 Node로 바로 추정하는 것이 아닙니다.

먼저 x1 Node의 오른쪽에 연결된 유사도가 큰 Node의 label을 먼저 추정합니다.

그리고 추정한 그 Node의 label을 가지고 굵은 선을 따라 또다시 바로 오른쪽의 Node의 label을 추정합니다.

이런 식으로 ‘이웃의 이웃’ 추정을 연속해서, 결국 x3 Node의 label을 추정하게 됩니다.

즉, x1 Node에서 x3로 한 번에 label을 추정하긴 어렵지만, 바로 옆의 유사한 Node를 통해 한 다리씩 건너서 추정하면(Indirect) 알고 싶은 label을 추정할 수 있습니다.

따라서 유사도는 Direct로 추정하기보다는 기본적으로 Indirect 방법으로 추정한다는 것을 알 수 있습니다.

그리고 label을 전파한다고 해서 label propagation으로 부르기도 합니다.

이와 관련된 예시는 아래의 손글씨 인식 그림을 통해서도 확인할 수 있습니다.

이처럼 Graph-based Learning의 가정은 두 Node가 유사하면(Edge 굵기가 굵으면, heavy Edge) 근처의 유사한 Node의 label과 동일한 label을 갖는 것이 합당하다는 것입니다.

이를 통해 기존의 Unlabeled Data의 Label이 무엇인지(Transductive Learning)를 추정하게 됩니다.

수학적 기호 정의와 Graph 종류 및 유사도 가중치 계산방식

그렇다면 실제로 Unlabeled Data에 대해 label을 찾기 위한 수학적 알고리즘은 어떻게 될까요?

이를 위해 우선 Graph에서의 Node와 Edge에 대한 수학적 Notation 정의를 내리게 됩니다.

Graph-based SSL에서 수학적으로 Label을 추정하는 방법1

우리가 알고 싶은 것은 기존에 가지고 있는 Unlabeled Data에 대한 label 값입니다.

앞에서 설명했듯이, Graph-based Semi-Supervised Learning의 label 추정 방법은 항상 기존에 알고 있는 label 값으로 추정하기 시작합니다.

따라서 기존 label과 추정 label로 각각 part를 나누어 생각해볼 수 있고 이때 minimum cut algorithm을 사용합니다.

minimum cut algorithm이란 Network Flow에서 등장하는 개념으로, 줄여서 mincut algorithm으로 부릅니다.

mincut algorithm은 네트워크식으로 연결된 Node들의 Edge에 따라 서로 다른 label을 가진 Node들로부터 오는 비용을 최소화하기 위해 Node들의 간선을 cut하는 방식입니다.

이때, Graph의 방식이 Direct인지 Indirect인지에 따라 cut하는 방식이 달라집니다.

Graph-based Semi-Supervised의 경우 Indirect Graph 방식이기 때문에 cut했을 때의 비용으로, cut하는 단순 간선의 개수가 될 수 있고, cut하는 간선의 가중치(Edge)의 합이 될 수도 있습니다.

본 내용의 경우, 유사도를 가중치로 계산하기 때문에 서로 다른 label을 갖는 Node의 간선을 cut해서 가중치의 합이 최소가 되는 방향으로 Graph가 구성되는 것을 알 수 있습니다.

조금 더 이해를 돕기 위해 아래의 그림 예시를 참고하시면 될 것 같습니다.

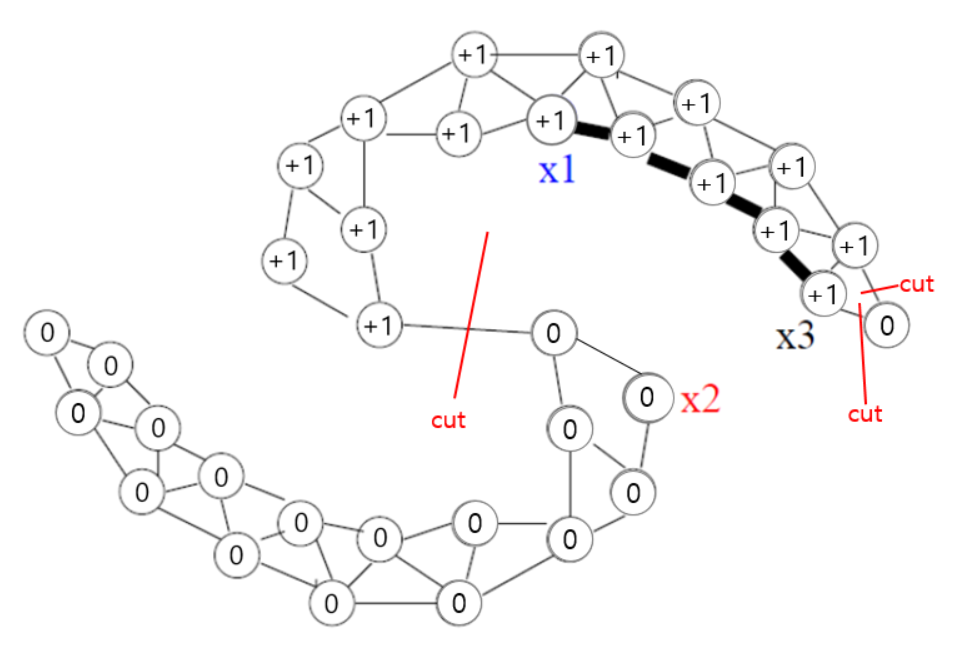
그리고 이를 수식화하면,

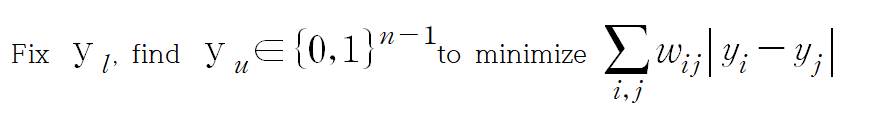
이 되고 우선 실제 label 값 y_l을 고정합니다.

이 말은 label을 알고 있는 Data는 항상 완벽해서 Noise나 Error가 전혀 없다고 보기 때문에, 기존 label은 반드시 유지해야 한다는 것을 의미합니다.

그러면서 추정하고 싶은 label y_i와 y_j에 대해서는 0 또는 1의 정수만 가질 수 있는 것도 의미합니다.

즉, 0~1 사이의 실숫값도 허용하지 않고 solution 자체가 0 아니면 1이어야 하는, 엄격한 기준을 세우고 있는 것입니다.

이렇게 두 가지 전제 조건 아래에, 유사도 w를 이용한 추정 label의 오차 절대 합이 최소가 되게 하는 것이 목적입니다.

만약 그 합이 클 때는 비용을 최소화하기 위해 Graph 상에서 cut 작업을 진행하게 됩니다.

그리고 이를 위해 최적화 문제로 바꾸어 해결하면,

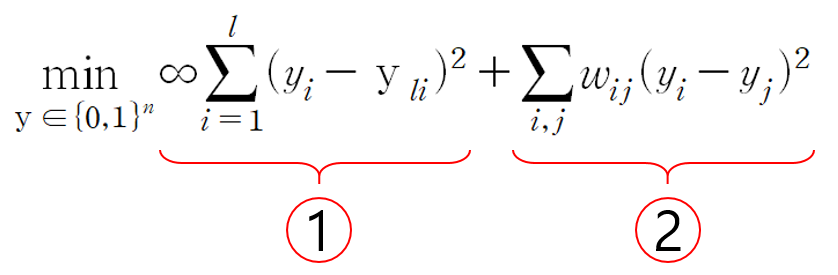
로 바꿔서 풀 수 있습니다.

그리고 이때 위의 그림대로 최소화할 각 항을 1번 part와 2번 part로 나누어 생각해볼 수 있습니다.

왜냐하면, 각각 기존 label과 추정 label에 해당하기 때문입니다.

우선, 1번 part에 해당하는 ‘기존 label part’는 추정 label y_i와 정답 label y_li가 모두 같으면 0, 하나라도 다르면 ∞ penalty를 부여하는 것을 의미합니다.

즉, 추정된 label과 정답 label이 조금이라도 다른 것을 허용하지 않겠다는 뜻입니다.

앞에서 기존 label y_l은 모두 완벽하다고 보고 그 값들을 모두 고정한 것과 일맥상통하는 대목입니다.

다음으로 2번 part에 해당하는 ‘추정 label part’는 서로 근처에 있고 유사한 Node들이면 그 Node들 사이의 label은, 최대한 같은 값이 되도록 만들라는 뜻입니다.

유사도가 클수록 근처의 Node들은 label이 서로 같아야 한다고 보는 Graph-based Learning의 가정을 담고 있다고 할 수 있습니다.

물론 이때, y_i 또는 y_j가 가질 수 있는 값은 0과 1뿐입니다.

Graph-based SSL에서 수학적으로 Label을 추정하는 방법2

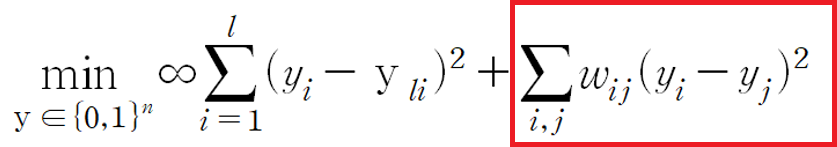
이번에는 Label을 추정하는 방법1에서 ‘추정 label part’에 해당하는 조건을 완화하여 label을 추정하는 방법입니다.

즉, 추정하려는 label이 항상 0 아니면 1이어야 한다는 정수 가정을 실수 가정으로 바꿔 완화하는 방법입니다.

이를 위해, Harmonic function f(x_i)=y_i를 사용합니다. 즉,

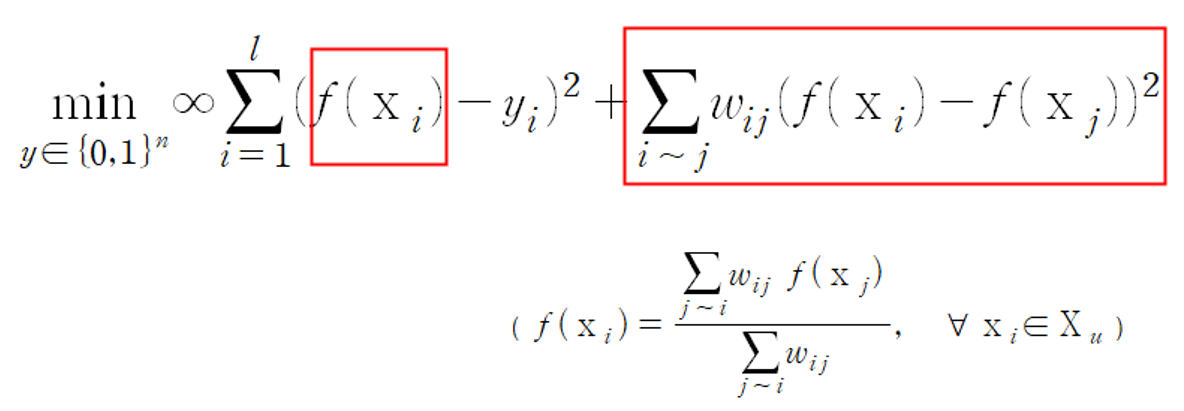
으로 바뀌게 됩니다.

두 Node i와 j의 label이 항상 0 또는 1은 아니어도 되지만, 유사도가 높을수록 Harmonic function 값이 반영된 f(x_i)실숫값과 f(x_j)실숫값이 서로 유사해야 합니다.

그리고 나중에 실제 label을 달 때는 cut-off를 정해서 그 기준으로 label을 확정 짓게 됩니다.

그런데, 이 ‘추정 label part’에 해당하는 계산과정에서 Graph Laplacian Matrix를 사용하면 비교적 간단하게 추정 label을 계산할 수 있게 됩니다.

Graph Laplacian Matrix를 이용한 방법2의 해 구하기

우리가 가지고 있는 Data에서, label이 있는 Data의 개수는 l이고 label 없는 Data의 개수는 u라 할 때 모든 Data의 개수는 l+u가 됩니다.

지금부터 설명할 대부분의 Matrix는 행 또는 열이 l+u인 행렬들로, label을 추정하는 두 번째 방법에서 ‘추정 label part’에 해당하는 식을 간단하게 계산하기 위해 아래의 행렬을 계산합니다.

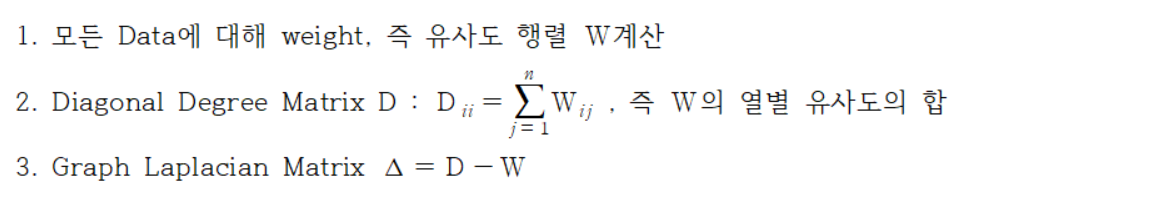
즉, Graph Laplacian Matrix를 구해서 ‘추정 label part’를 계산하면,

이 됩니다.

조금 더 쉬운 이해를 위해 예를 들어보겠습니다.

Data가 아래의 Graph(Node의 숫자는 각 Node의 label이 아닌 Node 번호)를 갖는 경우,

먼저 유사도 행렬 W를 Node간 연결이 된 경우에는 1, 그렇지 않으면 0인 방식(Adjacency Matrix)으로 계산합니다.

이어서 이 W의 열별 유사도의 합을 계산하고 Diagonal Degree Matrix D를 구하여 최종적으로 Graph Laplacian Matrix를 계산합니다.

이때, ‘추정 label part’ 식은

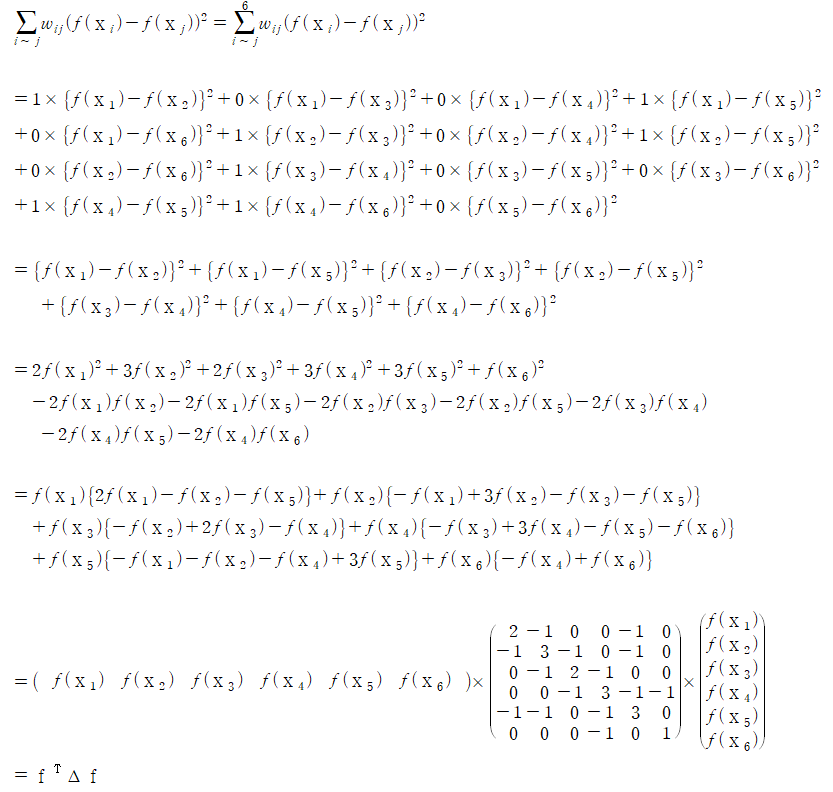
으로 표현할 수 있는 것을 확인할 수 있습니다.

한편, ‘추정 label part’의 Graph Laplacian Matrix를 이용해서 실제로 우리가 알고 싶은 label의 추정값(f_u) 부분만 쉽게 계산할 수도 있습니다.

바로 Partition Laplacian Matrix를 사용하는 것인데요, 이제부터 살펴보겠습니다.

그리고 Partition Laplacian을 적용하기 위해 ‘추정 label part’를 Harmonic Function Vector f에 대해 미분하면,

Graph-based SSL에서 수학적으로 Label을 추정하는 방법3

Graph-based SSL에서 수학적으로 Label을 추정하는 방법1과 방법2에서는 모두 ‘기존 label part’에서 실제 label을 그대로 적용했습니다.

그런데 사람들은 실제 Data에 Noise나 Error가 존재할 수 있기 때문에, 주어진 label이 항상 옳다고 할 수 있는지에 대해 의문을 갖기 시작했습니다.

따라서 ‘기존 label part’의 ∞ penalty 조건을 완화하기 시작합니다.

일부 주어진 label들이 틀린 label이면 그것을 보존하는 것보다는 틀림을 인지하고 수정하는 것이 더 좋은 결과물이 될 수 있다고 보기 때문입니다.

하지만, 제대로 된 기존 label을 바꾸는 것은 막아야 하므로 별도의 penalty 장치(λ)를 두게 되고 그 식은 다음과 같습니다.

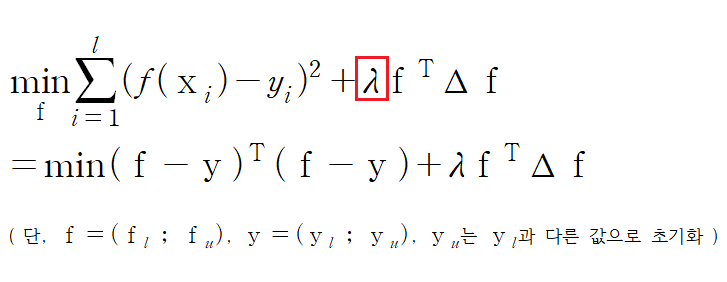
다시 말해서, ‘기존 label part’에서 ∞가 사라져 조건을 완화한 대신, 제대로 된 기존 label이 바뀌는 것은 막기 위해 penalty λ를 적용하게 됩니다.

이때, λ는 크게 할수록 실제 labeled Data의 label은 변할 가능성이 커지고 작게 할수록 실제 label을 보존하는 방향으로 설정됩니다.

그리고 이 방법이 가장 현실적으로 생각하고 적용할 수 있는 Graph-based Semi-Supervised Learning 방법이며 이에 대한 solution은 아래와 같습니다.

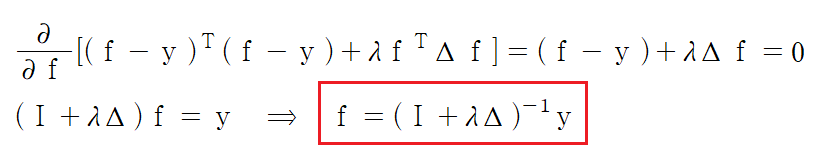
즉, Graph-based Semi-Supervised Learning에서는 기존에 가지고 있는 Data의 label을 추정하는데 수학적으로 항상 명시적인 해(explicit solution)가 존재한다는 것을 알 수 있습니다.

이제부터는 이러한 이론적 배경을 기반으로 Graph-based Semi-Supervised Learning을 Python으로 구현한 Code를 살펴보겠습니다.

Python Code for Graph-based Semi-Supervised Learning

본격적인 Code를 살펴보기에 앞서 서두에서 밝힌 것처럼, 해당 Code는 고려대학교 산업경영공학과 강필성 교수님의 강의자료를 바탕으로 작성됐음을 다시 한번 밝힙니다.

(https://github.com/pilsung-kang/Business-Analytics)

그럼 이제 본격적인 Code를 살펴보겠습니다.

import os
import numpy as np
import numpy.linalg as lin
import pandas as pd
import matplotlib.pyplot as plt
from scipy import sparse 
from scipy.sparse.linalg import inv
from scipy.spatial import distance

우선 필요한 패키지들을 설치하고 불러옵니다.

datafile = "~/Data1.csv"
data = pd.read_csv(datafile, engine="python")
Testdata = pd.read_csv(datafile, engine="python")
Testdata

Data를 불러와서 Training용 Data와 Test용 Data로 모두 할당합니다. 원래 Raw Data를 확인해보면,

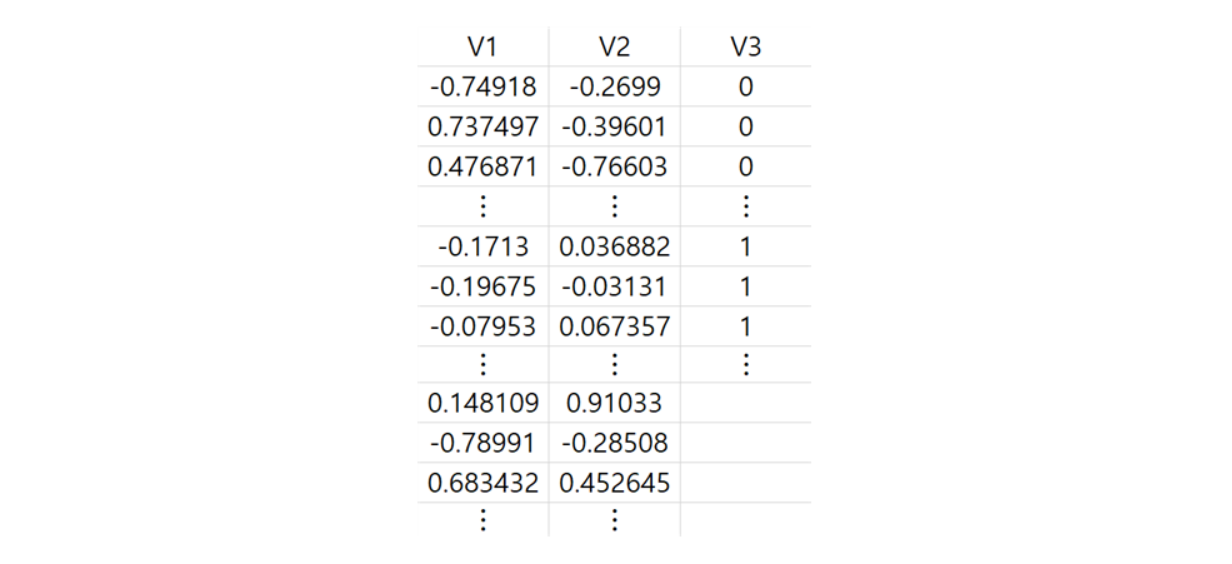
0과 1 두 개의 label class로 이루어진 2차원 Data와 label이 없는 2차원 Data로 구성된 것을 확인할 수 있습니다(V3).

label class 0 Data는 68개이고 label class 1 Data는 38개이며 label이 없는 Data는 104개, 총 210개로 이루어져 있습니다.

plt.scatter(Testdata['V1'],Testdata['V2'])
plt.show()

우선 label에 상관없이 Data를 시각화해보면,

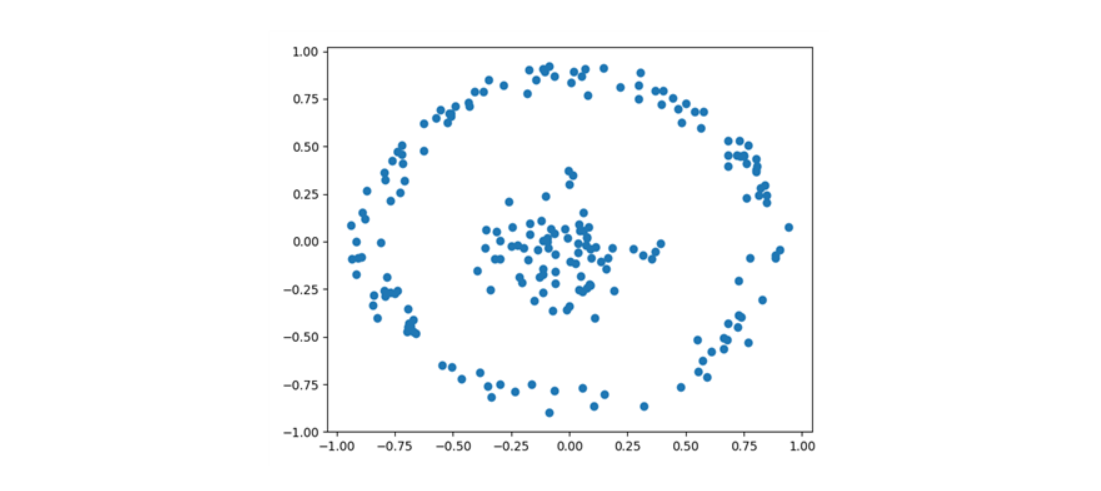
와 같이, 밀도 방식의 내외부 원형구조로 이루어진 것을 확인할 수 있습니다.

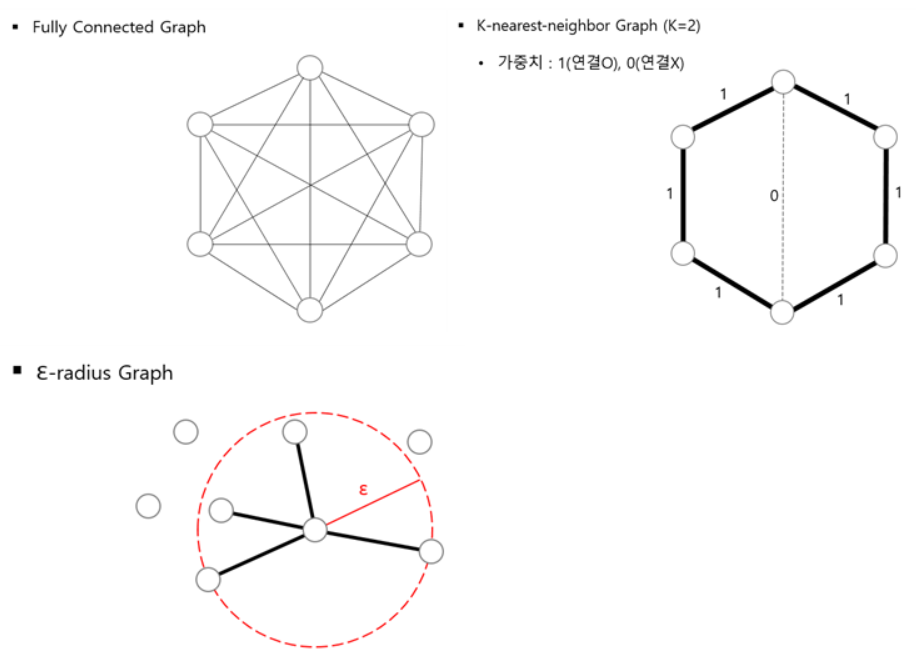
이러한 사실은 뒤에서 사용할 Graph로 ε-radius 방식을 적용해보게 되는 배경이 됩니다.

따라서 앞으로 흘러갈 code의 큰 흐름을 먼저 정리해보겠습니다.

이론 내용에서 완화 조건이 적용된 Graph-based SSL Label 추정 방법2와 방법3을 각각 적용하고 잘 labeling 되는지 확인해보겠습니다.

우선, 방법2에 대해서 살펴보겠습니다.

Python Code for Graph-based SSL에서 수학적으로 Label을 추정하는 방법2

1. label이 없는 Data에 대해 label 값을 추정하기 위해 우선 문자열인 각 label 값을 모두 숫자로 바꿉니다.

2. 그리고 기존의 label 값을 따로 행렬로 변환합니다. 그 이유는 마지막에 labeling 할 때 계산에 필요하기 때문입니다. (이론 내용의 Graph Laplacian Matrix part 참고)

3. 이어서 Laplacian Matrix로 label을 추정하기 위해 Weight Matrix를 계산합니다. 이때, ε-radius Graph를 사용하여 RBF Kernel로 Weight Matrix를 생성하기 위해 code로 ε-radius Graph 함수를 정의하고 Euclidean Distance를 이용한 Distance Matrix를 만들어 RBF Kernel 함수 정의에 사용합니다.

4. 계산된 Weight Matrix를 가지고 열(또는 행)마다 합을 계산하여 Diagonal Degree Matrix를 계산하면 최종적으로 Laplacian Matrix를 구할 수 있게 됩니다. 그리고 해당 Laplacian Matrix로 label을 추정하기 위해 Subset Matrix를 구성합니다.

5. 해당 Subset Matrix와 기존의 label 행렬을 가지고 Harmonic Function 값을 계산한 뒤, 사용자가 설정한 cut-off를 기준으로 labeling을 마무리하게 됩니다.

그럼 이제, 각 과정의 세부적인 code를 살펴보겠습니다.

1-1. label class를 나누어 각 class와 label 유무에 대한 index 정보를 저장합니다.

class0_idx = (data['V3'] == '0')
class1_idx = (data['V3'] == '0')
labeled_idx = (class0_idx | class1_idx)
unlabeled_idx = (labeled_idx != True)

1-2. 문자열(String) 정보를 숫자로 바꿔줍니다.

num_samples = data.shape[0]
num_samples # 210
y = np.zeros(shape=(num_samples)) y # 0을 210개 생성
y[class0_idx] = 0
y[class1_idx] = 1
y[unlabeled_idx] = 0.5
data['V3'] = y

임의의 숫자로 0 Data가 210개 있는 y Data를 생성 후, 순차적으로 label class 숫자 값을 할당합니다.

이는 기존에 불러온 Data의 label class 값이 숫자 형식이 아닌 문자열 형식의 정보(String)를 숫자로 바꿔주기 위함입니다.

따라서 기존에 정의한 data의 label class에 해당하는 세 번째 열 V3를 ‘숫자’ label class로 바꿔줍니다.

참고로 label이 없는 index 값은 실제 label 값과 겹치지 않기 위해 0.5 값을 가지도록 했습니다.

실제 label 값이 +1과 –1일 때 label이 없는 index 값을 0으로 하는 것과 유사합니다.

2. 기존의 label 값을 따로 행렬로 변환하고 label이 있는 Data의 길이 정보도 계산합니다. 그 이유는 나중에 Subset Laplacian Matrix를 구성하기 위함입니다.

length = len(y)
Yl = np.full((length,1),0)
Yl[class0_idx] = 0
Yl[class1_idx] = 1
labeled_length = len(y[labeled_idx])
labeled_length

이론에서도 언급했었던 실제 label 값을 행렬로 만들어 마지막에 label을 추정하기 위한 (Harmonic Function) 준비를 합니다.

이를 위해 앞의 code에서 할당했던 label class index 값들을 불러와 행렬을 구성합니다.

3-1. RBF kernal 함수에 사용할 Euclidean Distance Matrix를 만들어 줍니다.

data.iloc[:, :2]
euc = distance.cdist(data.iloc[:, :2], data.iloc[:, :2], 'sqeuclidean')

3-2. ε-radius Graph 함수를 정의하고 Euclidean Distance를 이용한 Distance Matrix를 만들어 RBF Kernel 함수 정의에 사용합니다. 반지름 ε이 0보다 작거나 같을 수는 없고 0보다 클 때 실제 Euclidean Distance가 ε보다 작거나 같은 Node들만 연결 고려대상으로 합니다.

def e_radius(euc, epsilon):
    if epsilon <= 0:
        print('Use epsilon >= 0')
        return None
    e_distance = np.where(euc <= epsilon, euc, np.inf)
    return e_distance

3-3. ε-radius Graph에서 연결된 Node들 간 거리를 반환받아 그 거리 정보를 가지고 RBF Kernel이 적용된 Matrix를 반환합니다.

def RBF_Weight(euc, epsilon, gamma):
    euc = e_radius(euc, epsilon)
   
    #RBF
    w_matrix = np.exp(-euc*gamma) #시그마 제곱 대신 gamma를 사용한다(시그마 제곱의 역수).
    np.fill_diagonal(w_matrix,0)
    return w_matrix

3-4. ε-radius Graph와 RBF Kernel을 이용해 Graph의 원의 반지름이 1, RBF Kernel에서 gamma값이 20인 Weight Matrix를 계산합니다.

W = RBF_Weight(euc, epsilon = 1, gamma = 20)

4-1. 계산된 Weight Matrix를 가지고 열(또는 행)마다 합을 계산하고 원소들을 대각화해서 Diagonal Degree Matrix를 구합니다.

colsum = W.sum(axis=1)
D = sparse.diags(colsum)

4-2. Diagonal Degree Matrix에서 Weight Matrix를 빼서 최종적인 Laplacian Matrix를 구합니다.

L = D - W

4-3. 앞 2번 code에서 label이 있는 Data의 길이 정보를 가져와 Subset Laplacian Matrix를 구성합니다.

Luu = L[labeled_length:,labeled_length:]
Lul = L[labeled_length:,:labeled_length]

5-1. 해당 Subset Matrix와 2번 code에서 계산한 기존의 label 행렬을 가지고 Unlabeled Harmonic Function 값을 계산합니다.

Fu = -lin.inv(Luu)*Lul*Yl[labeled_idx]

5-2. 사용자가 설정한 cut-off(여기서는 0.5)를 기준으로 labeling을 마무리하게 됩니다.

Fu_lenght = len(Fu)
for i in range(Fu_lenght):
    if Fu[i,0] >= 0.5:
        Fu[i,0] = 1
    else:
        Fu[i,0] = 0

5-3. 새로 부여된 label을 Data에 추가하여 시각화합니다. 비교를 위해 우선 labeling 전 Data의 시각화 자료를 살펴보겠습니다.

Total_y_length = len(y[class0_idx]) + len(y[class1_idx]) + len(y[unlabeled_idx])
Total_y =  np.full((Total_y_length,1),0)
Total_y[class0_idx] = 0
Total_y[class1_idx] = 1
Total_y[unlabeled_idx] = Fu 
Testdata['V3'] = Total_y
Testdata

plt.scatter(data['V1'],data['V2'],c=data['V3'])
plt.show()

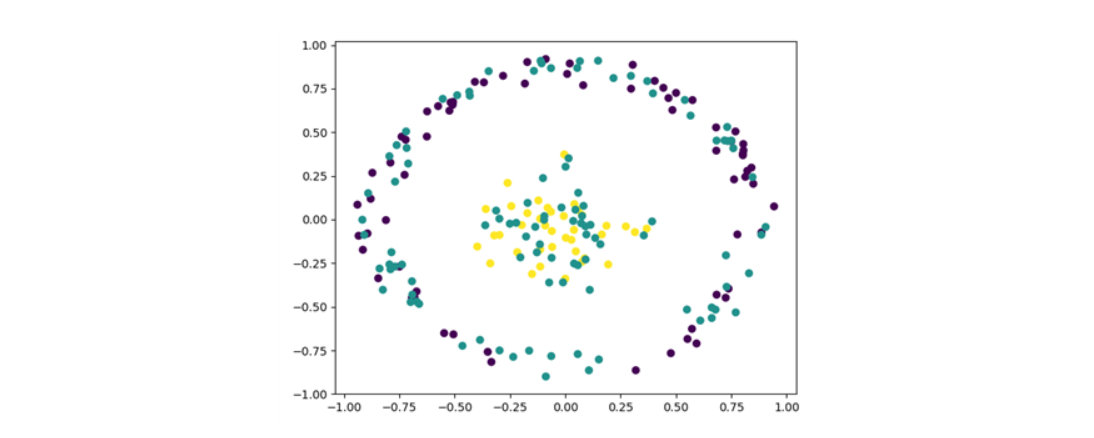
다음으로 labeling 한 Data를 시각화하면,

plt.scatter(Testdata['V1'],Testdata['V2'],c=Testdata['V3'])
plt.show()

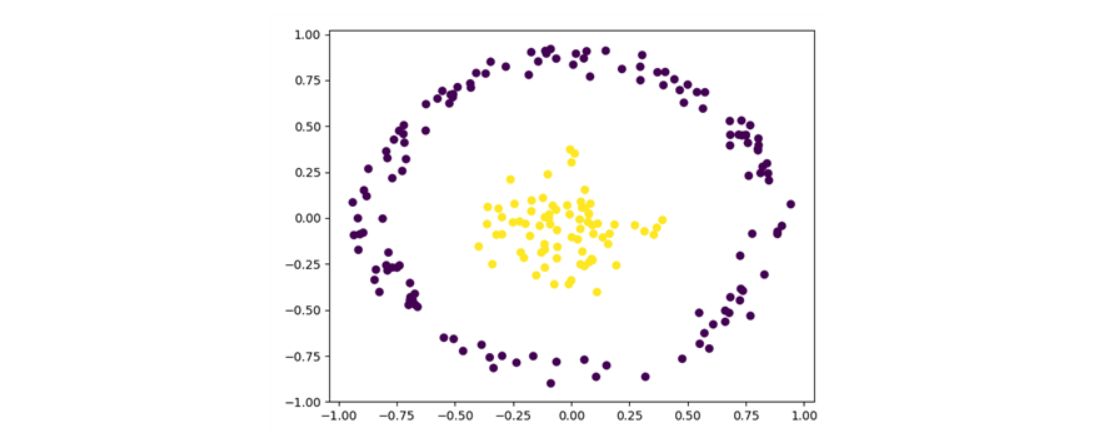
이처럼 잘 labeling된 것을 확인할 수 있습니다.

Python Code for Graph-based SSL에서 수학적으로 Label을 추정하는 방법3

Graph-based SSL에서 수학적으로 Label을 추정하는 방법2와 다르게 이번에는 실제 label 값도 함께 control 해보겠습니다.

1. 방법3에서 결론지었던 명시적 해를 구하는데 필요한 요소들인 단위행렬 I, λ, Laplacian Matrix, 실제 label vector를 구해보겠습니다.

I = sparse.eye(L.shape[0])
Lam = 2.0
L  # 방법2에서 이미 계산완료
YL = np.full((len(y),1),0)
YL[class0_idx] = 0
YL[class1_idx] = 1
YL[unlabeled_idx] = 0.5

Fu_ = lin.inv(I + Lam*L)*YL

2. cut-off 0.4를 기준으로 labeling하고 이때, 기존 label도 바뀔 수 있는 상황입니다.

Fu__length = len(Fu_)
for i in range(Fu__length):
    if Fu_[i,0] >= 0.4:
        Fu_[i,0] = 1
    else:
        Fu_[i,0] = 0

3. λ값이 반영된 기존 label에 대한 추정값과 모르던 label에 대한 추정값을 모두 산출하여 Data에 최종적으로 labeling 합니다.

Total_y_length_ = len(y[class0_idx]) + len(y[class1_idx]) + len(y[unlabeled_idx])
Total_y_ =  np.full((Total_y_length_,0),0)
Total_y_ = Fu_ 
Testdata['V3'] = Total_y_

4. labeling 잘 됐는지 시각화를 통해 확인하면,

plt.scatter(Testdata['V1'],Testdata['V2'],c=Testdata['V3'])
plt.show()

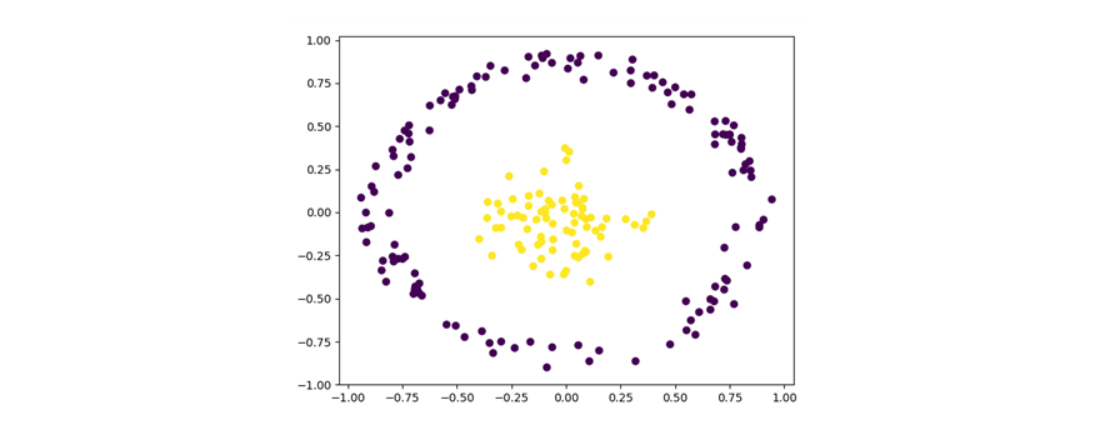
방법2 때와 마찬가지로 잘 labeling된 것을 확인할 수 있습니다.

Graph-based Semi-Supervised Learning 요약

이제 Posting 내용을 요약하면서 마무리하겠습니다.

Graph-based Semi-Supervised Learning은 가지고 있는 Data 가운데 label 없는 Data의 label을 알고 싶은 Transductive Learning이고 이를 알기 위해 Graph 방법을 사용합니다.

그리고 그 Graph를 가지고 Node들 사이의 유사도 가중치(Similarity Weight, Edge)가 큰 이웃의 이웃의 … 이웃을 이용하여 label을 추정합니다.

이때, 가지고 있는 Data의 모양에 따라 사용할 Graph를 정합니다.

가중치 계산방식은 단순 Node 연결 여부가 될 수도 있고 거리계산 방식이 될 수도 있습니다.

결국은 비용의 합이 최소가 되는 방향을 지향하면서 label을 추정합니다.

한편, 추정할 label 값을 특정 label 값으로 엄격하게 한정 지을지에 대한 여부와 기존 Data의 label이 틀릴 수도 있음을 허용할지 말지에 따라 label을 추정하는 방법은 조금씩 달라집니다.

하지만 어떤 방법이든 항상 명시적인 해가 존재합니다.

따라서 Graph-based Semi-Supervised Learning은 가지고 있는 Data의 label이 궁금할 때 합리적으로 적용해볼 수 있는 기계학습 방법입니다.

긴 글 읽어주셔서 감사합니다.

# label
# Transductive Learning
# Graph
# Node
# Similarity Weight (Edge)
# 기존 label
# 추정 label
# 엄격
# 완화
# Laplacian Matrix
# Explicit Solution

BYUN's Blog

My name is junhyung BYUN.